Đánh giá hiệu quả vốn đầu tư là tiền đề quan trọng cho việc quyết định lựa chọn phương án đầu tư của doanh nghiệp. Các hàm đánh giá hiệu quả vốn đầu tư đơn giản, nhanh chóng và chính xác trong Excel cũng sẽ là một lựa chọn khôn ngoan cho các nhà quản trị tài chính của doanh nghiệp.
Excel cung cấp cho chúng ta một nhóm các hàm tính toán giá trị dòng tiền như FV, PV, PMT.
Excel cung cấp cho chúng ta một nhóm các hàm tính toán giá trị dòng tiền như FV, PV, PMT.
Quy ước:
- P (Present Value) là giá trị hiện tại của tiền
- P (Present Value) là giá trị hiện tại của tiền
- F (Future Value) là giá trị tương lai của tiền
- i là tỉ suất (nếu vay vốn để đầu tư thì i là lãi suất vay, nếu vay từ nhiều nguồn với lãi suất khác nhau thì i là lãi suất vay bình quân từ các nguồn).
- A là khoản tiền được phát sinh ở một thời đoạn (là khoản thanh toán đều cho từng kỳ với lãi suất cố định)
- n là số thời đoạn (năm, quý, tháng)
1. Hàm FV (Future Value)
- Tính giá trị tương lai của một khoản đầu tư có lãi suất cố định trả theo định kỳ hoặc gửi thêm vào.
- Cú pháp: =FV(rate, nper, pmt, pv, type)
Trong đó:
+ rate là lãi suất mỗi kỳ
+ nper là tổng số kỳ tính lãi
+ pmt là số tiền phải trả đều trong mỗi kỳ, nếu bỏ trống thì coi là 0
+ pv là giá trị hiện tại của khoản đầu tư, nếu bỏ trống thì coi là 0
+ type là hình thức thanh toán. Nếu type = 1 thì thanh toán đầu kỳ (niên kim đầu kỳ), nếu type = 0 thì thanh toán vào cuối mỗi kỳ (mặc định)
Ví dụ: Tính số tiền một người gửi 10 000$ vào ngân hàng và mỗi năm gửi thêm 200$ với lãi suất 5%/năm (bỏ qua lạm phát) sau 10 năm như trong hình sau:
4. Các công thức khác có liên quan
Ngoài các công thức tính toán giá trị của dòng tiền ta còn có một số các công thức khác có liên quan như: tính lãi suất danh nghĩa, tính lãi suất thực tế, tính giá trị tương lai của một khoản đầu tư khi lãi suất thay đổi, tính khoản lãi phải trả…
Excel cũng cung cấp một nhóm các hàm tương ứng với các công thức đó.
4.1 Hàm EFFECT
- Tính lãi suất thực tế hàng năm cho một khoản đầu tư
- Cú pháp: =EFFECT(Nominal_rate, npery)
Trong đó:
+ Nominal_rate là lãi suất danh nghĩa
+ npery là số kỳ tính lãi trong năm
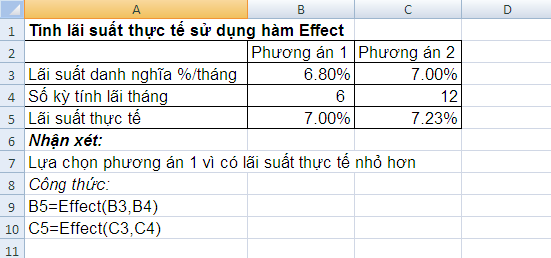
Ví dụ: Có 2 phương án vay tiền với mức lãi suất danh nghĩa và số lần tính lãi tương ứng cho theo bảng. Hãy lựa chọn phương án vay.
Để chọn phương án vay, sử dụng hàm EFFECT tính xem phương án nào có lãi suất thực tế nhỏ hơn thì sẽ lựa chọn. Việc tính toán được trình bày trong bảng sau:
- Tính giá trị tương lai của một khoản đầu tư khi lãi suất thay đổi.
- Cú pháp: =FVSCHEDULE(principal, schedule)
Trong đó:
+ principal là giá trị hiện tại của một khoản đầu tư
+ schedule là một dãy lãi suất được áp dụng
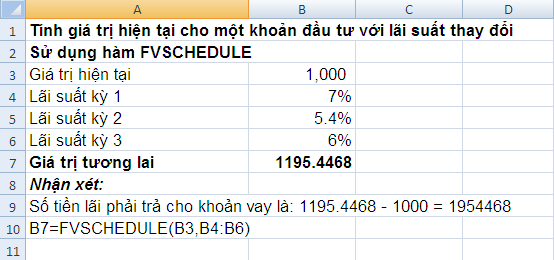
Ví dụ: Tính số tiền lãi phải trả cho một khoản vay 1000$ có lãi suất thay đổi theo các kỳ lần lượt là 7%, 5.4%, 6% . Sử dụng hàm FVSCHEDULE ta có:
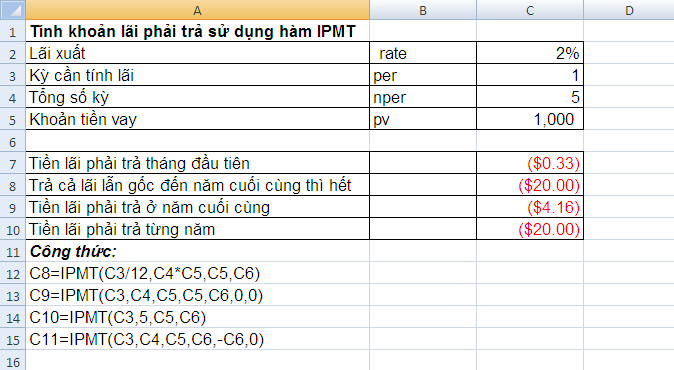
Ví dụ: Nếu vay ngân hàng một khoản tiền 1000$ với lãi suất 2%/năm (lãi kép) trong 5 năm thì lượng tiền phải trả lãi mỗi năm là bao nhiêu?
Giải: Sử dụng hàm IPMT ta có:
4.5 Hàm RATE
- Tính lãi suất cho một khoản vay.
- Cú pháp: =RATE(nper, pmt, pv, fv, type)
Các tham số tương tự như các hàm ở trên.
Ví dụ: Tính lãi suất cho một khoản vay 1000$ trong 2 năm, mỗi năm phải trả 100$. Đáo hạn phải trả cả gốc lẫn lãi là 1200$.
Giải: Sử dụng hàm RATE ta tính lãi suất của khoản vay đó là:
= RATE(2,100,-1000,1200,0)
=19%
5. Hàm NPV và IRR
Để đánh giá tính khả thi về mặt tài chính của một dự án đầu tư về lý thuyết cũng như thực tiễn người ta thường sử dụng 4 phương pháp sau:
- Phương pháp giá trị hiện tại thuần (NPV)
- Phương pháp tỷ suất thu hồi nội bộ (IRR)
- Thời gian hoàn vốn (PP)
- Chỉ số doanh lợi (PI)
Tuy nhiên, người ta thường dùng hai phương pháp giá trị hiện tại thuần và tỷ suất thu hồi nội bộ. Excel cũng cung cấp cho chúng ta hai hàm tính toán tương ứng là NPV và IRR.
5.1 Hàm NPV (Net Present Value)
- Giá trị hiện tại thuần của một dự án đầu tư là giá trị của các khoản đầu tư, chi phí và thu nhập trong vòng đời của dự án được quy về hiện tại.
- Cú pháp: =NPV(rate,value1,value2,…,value(n))
Trong đó:
+ rate là tỷ suất chiết khấu
+ value1 là giá trị vốn đầu tư ban đầu (biểu diễn dưới dạng số âm),
+ value2,…,value(n) luồng tiền kỳ vọng trong tương lai
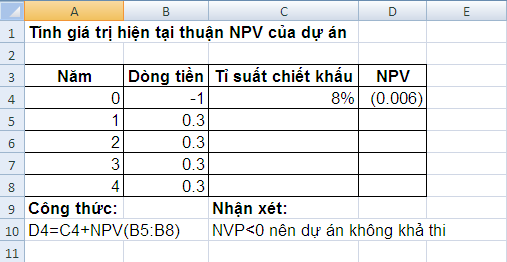
Ví dụ: Tính NPV cho một dự án đầu tư có đầu tư ban đầu là 1 tỉ đồng, doanh thu hàng năm là 0.5 tỉ, chi phí hàng năm là 0.2 tỉ, thời gian thực hiện dự án là 4 năm, có lãi suất chiết khấu là 8%/năm.
Sử dụng hàm NPV như sau:
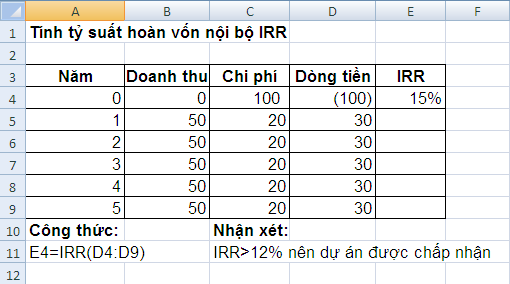
Ví dụ 3.15: Một dự án đầu tư tính đến thời điểm dự án bắt đầu đi vào hoạt động sản xuất là 100 triệu USD, doanh thu hàng năm của dự án là 50 triệu USD.
Chi phí hàng năm là 20 triệu USD, đời của dự án là 5 năm. Hãy xác định tỷ suất hoàn vốn nội bộ biết lãi suất vay dài hạn là 12%/năm.
Giải: Sử dụng hàm IRR xác định tỷ suất hoàn vốn nội bộ như sau:
6. CÁC HÀM TÍNH GIÁ TRỊ ĐẦU TƯ CHỨNG KHOÁN
Đầu tư vào chứng khoán cũng là một lĩnh vực đầu tư tài chính hết sức quan trọng của doanh nghiệp. Chính vì thế việc tính toán lãi suất đầu tư chứng khoán là hết sức cần thiết.
Để việc tính toán đơn giản, nhanh chóng và chính xác hơn Excel cung cấp một số hàm tính toán giá trị đầu tư như hàm ACCRINTM, INTRATE, RECEIVED…
Các tham số ngày tháng của các hàm tính giá trị chứng khoán trong Excel đều được đưa vào dưới dạng một chuỗi số tuần tự. Để đổi ngày tháng ra chuỗi số tuần tự ta nên dùng hàm DATE(year,month, day).
6.1 Hàm ACCRINTM (Accrued Interest at Maturity)
- Tính lãi gộp cho một chứng khoán trả vào ngày tới hạn
- Cú pháp: = ACCRINTM(issue, maturity, rate, par, basis)
Trong đó:
+ issue là ngày phát hành
+ maturity là ngày tới hạn
+ rate là tỷ suất của cuốn phiếu
+ par là giá trị mỗi cuốn phiếu. Nếu bỏ qua Excel sẽ gán là $1000
+ basis là số ngày cơ sở. Nếu basis = 0 thì năm có 360 ngày, basis = 1 thì năm có 365 ngày.
Ví dụ: Tính lãi gộp cho một trái phiếu kho bạc phát hành ngày 15/02/2005 và ngày tới hạn là 18/03/2006 có tỷ suất là 4%/năm và giá trị cuốn phiếu là 1000$. (tính một năm có 365 ngày).
Sử dụng hàm ACCRINTM
=ACCRINTM("02/15/05","03/18/06",0.04,1000,1)
= 43.397 $
6.2 Hàm INTRATE (Interest Rate)
- Tính lãi suât của một chứng khoán được đầu tư hết.
- Cú pháp:
=INTRATE(settlement, maturity, investment, redemption, basis)
Trong đó:
+ settlement là ngày thanh toán
+ maturity là ngày tới hạn
+ investment khoản tiền đầu tư
+ redemption là khoản tiền thu được vào ngày tới hạn
+ basis là số ngày cơ sở
Chú ý: Cần phân biệt giữa ngày thanh toán và ngày tới hạn. Nếu có một trái phiếu chính phủ có thời hạn là 5 năm được phát hành ngày 01/04/2000 và 1 tháng sau thì có người mua chứng khoán này thì ngày thanh toán là 01/05/2000 và ngày tới hạn là 01/04/2005.
Ví dụ: Tính lãi suất cho một chứng khoán có ngày thanh toán là 01/02/2005, ngày tới hạn là 18/06/2006, tiền đầu tư là 10 000$, tiền thu được là 12 000$, cơ sở là 0.
Sử dụng hàm INTRATE ta tính được lãi suất như sau:
=INTRATE("02/01/05","06/18/06",10000,12000,0)
=0.145
6.3 Hàm RECEIVED
- Tính số tiền thu được vào ngày tới hạn của một chứng khoán được đầu tư hết.
- Cú pháp:
=RECEIVED(settlement, maturity, investment, discount, basis)
Trong đó: discount là tỷ suất chiết khấu, các tham số khác tương tự hàm INTRATE
Ví dụ: Tính số tiền thu được vào ngày tới hạn của một tín phiếu kho bạc được đầu tư hết có ngày thanh toán là 18/05/2004, ngày tới hạn là 18/07/2006, tiền đầu tư là 20 000$, tỷ suất chiết khấu là 5.85%, cơ sở là 1.
Sử dụng hàm RECEIVED ta có:
=RECEIVED("05/18/04","07/18/06",20000,5.85%,1)
=22 900.6$
6.4 Hàm DISC (Discount)
- Tính tỷ suất chiết khấu của một chứng khoán.
- Cú pháp: =DISC(settlement, maturity, pr, redemption, basis)
Trong đó:
+ pr là giá trị mỗi 100$ mệnh giá của chứng khoán
+ redemption là giá trị phải trả cho mỗi chứng khoán 100$
+ các tham số khác tương tự như ở trên
Ví dụ: Tính tỷ suất chiết khấu cho một trái phiếu được mua lại ngày 12/05/2005 có ngày tới hạn là 19/05/2006, mua 96.18$ cho mệnh giá 100$, giá trị phải trả là 100$.
Sử dụng hàm DISC ta có:
=DISC("05/12/05","05/19/06",96.18,100,1)
=0.037
1. Hàm FV (Future Value)
- Tính giá trị tương lai của một khoản đầu tư có lãi suất cố định trả theo định kỳ hoặc gửi thêm vào.
- Cú pháp: =FV(rate, nper, pmt, pv, type)
Trong đó:
+ rate là lãi suất mỗi kỳ
+ nper là tổng số kỳ tính lãi
+ pmt là số tiền phải trả đều trong mỗi kỳ, nếu bỏ trống thì coi là 0
+ pv là giá trị hiện tại của khoản đầu tư, nếu bỏ trống thì coi là 0
+ type là hình thức thanh toán. Nếu type = 1 thì thanh toán đầu kỳ (niên kim đầu kỳ), nếu type = 0 thì thanh toán vào cuối mỗi kỳ (mặc định)
Ví dụ: Tính số tiền một người gửi 10 000$ vào ngân hàng và mỗi năm gửi thêm 200$ với lãi suất 5%/năm (bỏ qua lạm phát) sau 10 năm như trong hình sau:
2. Hàm PV (Present Value)
- Trả về giá trị hiện tại của một khoản đầu tư theo từng kỳ.
- Cú pháp: =PV(rate, nper, pmt, fv, type)
Trong đó: fv là giá trị tương lai của khoản đầu tư và các tham số tương tự như hàm FV .
Ví dụ: Một người muốn có số tiền tiết kiệm 300$ sau năm 10 năm. Hỏi bây giờ người đó phải gửi vào ngân hàng bao nhiêu? biết lãi suất ngân hàng là 6%/năm (bỏ qua lạm phát)
Áp dụng hàm PV ta có:
3. Hàm PMT (Payment)
- Trả về khoản tương đương từng kỳ cho một khoản đầu tư có lãi suất cố định trả theo định kỳ.
- Cú pháp: =PMT(rate, nper, pv, fv, type)
Các tham số tương tự như các hàm trên.
Ví dụ: Một người muốn có khoản tiền tiết kiệm 50 triệu đồng sau 5 năm thì người đó phải gửi vào ngân hàng mỗi tháng bao nhiêu tiền? Biết lãi suất ngân hàng là 8%/năm (bỏ qua lạm phát).
Giải: Số tiền người đó phải gửi mỗi tháng được tính như trong hình sau:
4. Các công thức khác có liên quan
Ngoài các công thức tính toán giá trị của dòng tiền ta còn có một số các công thức khác có liên quan như: tính lãi suất danh nghĩa, tính lãi suất thực tế, tính giá trị tương lai của một khoản đầu tư khi lãi suất thay đổi, tính khoản lãi phải trả…
Excel cũng cung cấp một nhóm các hàm tương ứng với các công thức đó.
4.1 Hàm EFFECT
- Tính lãi suất thực tế hàng năm cho một khoản đầu tư
- Cú pháp: =EFFECT(Nominal_rate, npery)
Trong đó:
+ Nominal_rate là lãi suất danh nghĩa
+ npery là số kỳ tính lãi trong năm
Ví dụ: Có 2 phương án vay tiền với mức lãi suất danh nghĩa và số lần tính lãi tương ứng cho theo bảng. Hãy lựa chọn phương án vay.
Để chọn phương án vay, sử dụng hàm EFFECT tính xem phương án nào có lãi suất thực tế nhỏ hơn thì sẽ lựa chọn. Việc tính toán được trình bày trong bảng sau:
4.2 Hàm NOMINAL
- Đây là hàm tính ngược của hàm EFFECT. Tính lãi suất danh nghĩa hàng năm cho một khoản đầu tư.
- Cú pháp: =NOMINAL(Effect_rate, npery)
Trong đó:
+ Effect_rate là lãi suất thực tế
+ npery là số kỳ tính lãi trong năm
4.3 Hàm FVSCHEDULE- Tính giá trị tương lai của một khoản đầu tư khi lãi suất thay đổi.
- Cú pháp: =FVSCHEDULE(principal, schedule)
Trong đó:
+ principal là giá trị hiện tại của một khoản đầu tư
+ schedule là một dãy lãi suất được áp dụng
Ví dụ: Tính số tiền lãi phải trả cho một khoản vay 1000$ có lãi suất thay đổi theo các kỳ lần lượt là 7%, 5.4%, 6% . Sử dụng hàm FVSCHEDULE ta có:
4.4 Hàm IPMT (Interest Payment)
- Tính khoản lãi phải trả trong một khoảng thời gian cho một khoản đầu tư có lãi suất cố định trả theo định kỳ cố định.
- Cú pháp: =IPMT(rate, per, nper, pv, fv, type)
Trong đó:
+ rate là lãi suất cố định
+ per là khoảng thời gian cần tính lãi
+ nper tổng số lần thanh toán
+ pv là khoản tiền vay hiện tại
+ fv là khoản tiền còn lại khi đến kỳ thanh toán.
+ type là kiểu thanh toán. Nếu type = 1 thì thanh toán đầu kỳ (niên kim đầu kỳ), nếu type = 0 thì thanh toán vào cuối kỳ (mặc định)Ví dụ: Nếu vay ngân hàng một khoản tiền 1000$ với lãi suất 2%/năm (lãi kép) trong 5 năm thì lượng tiền phải trả lãi mỗi năm là bao nhiêu?
Giải: Sử dụng hàm IPMT ta có:
- Tính lãi suất cho một khoản vay.
- Cú pháp: =RATE(nper, pmt, pv, fv, type)
Các tham số tương tự như các hàm ở trên.
Ví dụ: Tính lãi suất cho một khoản vay 1000$ trong 2 năm, mỗi năm phải trả 100$. Đáo hạn phải trả cả gốc lẫn lãi là 1200$.
Giải: Sử dụng hàm RATE ta tính lãi suất của khoản vay đó là:
= RATE(2,100,-1000,1200,0)
=19%
5. Hàm NPV và IRR
Để đánh giá tính khả thi về mặt tài chính của một dự án đầu tư về lý thuyết cũng như thực tiễn người ta thường sử dụng 4 phương pháp sau:
- Phương pháp giá trị hiện tại thuần (NPV)
- Phương pháp tỷ suất thu hồi nội bộ (IRR)
- Thời gian hoàn vốn (PP)
- Chỉ số doanh lợi (PI)
Tuy nhiên, người ta thường dùng hai phương pháp giá trị hiện tại thuần và tỷ suất thu hồi nội bộ. Excel cũng cung cấp cho chúng ta hai hàm tính toán tương ứng là NPV và IRR.
5.1 Hàm NPV (Net Present Value)
- Giá trị hiện tại thuần của một dự án đầu tư là giá trị của các khoản đầu tư, chi phí và thu nhập trong vòng đời của dự án được quy về hiện tại.
- Cú pháp: =NPV(rate,value1,value2,…,value(n))
Trong đó:
+ rate là tỷ suất chiết khấu
+ value1 là giá trị vốn đầu tư ban đầu (biểu diễn dưới dạng số âm),
+ value2,…,value(n) luồng tiền kỳ vọng trong tương lai
Ví dụ: Tính NPV cho một dự án đầu tư có đầu tư ban đầu là 1 tỉ đồng, doanh thu hàng năm là 0.5 tỉ, chi phí hàng năm là 0.2 tỉ, thời gian thực hiện dự án là 4 năm, có lãi suất chiết khấu là 8%/năm.
Sử dụng hàm NPV như sau:
5.2 Hàm IRR (Internal Rate of Return)
- Tỉ suất thu hồi nội bộ IRR (hay tỉ suất hoàn vốn nội bộ) là mức lãi suất nếu dùng nó làm suất chiết khấu để tính chuyển các khoản thu chi của dự án về cùng mặt bằng thời gian hiện tại thì tổng thu sẽ cân bằng với tổng chi, tức là NPV = 0.
- Đánh giá:
+ nếu IRR >= r thì dự án được chấp nhận
+ nếu IRR < r thì dự án không được chấp nhận
Excel cũng cung cấp hàm tính IRR.
- Cú pháp: =IRR(value,guess)
Trong đó:
+ value là giá trị vốn đầu tư ban đầu (biểu diễn dưới dạng số âm)
+ guess là giá trị suy đoán, nếu bỏ trống thì được gán là 10%
Trong Excel cũng dùng phương pháp thử dần. Nếu sau 20 lần thử không tính được thì báo lỗi #NUM. Thay đổi giá trị dự đoán để Excel tính lại.Ví dụ 3.15: Một dự án đầu tư tính đến thời điểm dự án bắt đầu đi vào hoạt động sản xuất là 100 triệu USD, doanh thu hàng năm của dự án là 50 triệu USD.
Chi phí hàng năm là 20 triệu USD, đời của dự án là 5 năm. Hãy xác định tỷ suất hoàn vốn nội bộ biết lãi suất vay dài hạn là 12%/năm.
Giải: Sử dụng hàm IRR xác định tỷ suất hoàn vốn nội bộ như sau:
6. CÁC HÀM TÍNH GIÁ TRỊ ĐẦU TƯ CHỨNG KHOÁN
Đầu tư vào chứng khoán cũng là một lĩnh vực đầu tư tài chính hết sức quan trọng của doanh nghiệp. Chính vì thế việc tính toán lãi suất đầu tư chứng khoán là hết sức cần thiết.
Để việc tính toán đơn giản, nhanh chóng và chính xác hơn Excel cung cấp một số hàm tính toán giá trị đầu tư như hàm ACCRINTM, INTRATE, RECEIVED…
Các tham số ngày tháng của các hàm tính giá trị chứng khoán trong Excel đều được đưa vào dưới dạng một chuỗi số tuần tự. Để đổi ngày tháng ra chuỗi số tuần tự ta nên dùng hàm DATE(year,month, day).
6.1 Hàm ACCRINTM (Accrued Interest at Maturity)
- Tính lãi gộp cho một chứng khoán trả vào ngày tới hạn
- Cú pháp: = ACCRINTM(issue, maturity, rate, par, basis)
Trong đó:
+ issue là ngày phát hành
+ maturity là ngày tới hạn
+ rate là tỷ suất của cuốn phiếu
+ par là giá trị mỗi cuốn phiếu. Nếu bỏ qua Excel sẽ gán là $1000
+ basis là số ngày cơ sở. Nếu basis = 0 thì năm có 360 ngày, basis = 1 thì năm có 365 ngày.
Ví dụ: Tính lãi gộp cho một trái phiếu kho bạc phát hành ngày 15/02/2005 và ngày tới hạn là 18/03/2006 có tỷ suất là 4%/năm và giá trị cuốn phiếu là 1000$. (tính một năm có 365 ngày).
Sử dụng hàm ACCRINTM
=ACCRINTM("02/15/05","03/18/06",0.04,1000,1)
= 43.397 $
6.2 Hàm INTRATE (Interest Rate)
- Tính lãi suât của một chứng khoán được đầu tư hết.
- Cú pháp:
=INTRATE(settlement, maturity, investment, redemption, basis)
Trong đó:
+ settlement là ngày thanh toán
+ maturity là ngày tới hạn
+ investment khoản tiền đầu tư
+ redemption là khoản tiền thu được vào ngày tới hạn
+ basis là số ngày cơ sở
Chú ý: Cần phân biệt giữa ngày thanh toán và ngày tới hạn. Nếu có một trái phiếu chính phủ có thời hạn là 5 năm được phát hành ngày 01/04/2000 và 1 tháng sau thì có người mua chứng khoán này thì ngày thanh toán là 01/05/2000 và ngày tới hạn là 01/04/2005.
Ví dụ: Tính lãi suất cho một chứng khoán có ngày thanh toán là 01/02/2005, ngày tới hạn là 18/06/2006, tiền đầu tư là 10 000$, tiền thu được là 12 000$, cơ sở là 0.
Sử dụng hàm INTRATE ta tính được lãi suất như sau:
=INTRATE("02/01/05","06/18/06",10000,12000,0)
=0.145
6.3 Hàm RECEIVED
- Tính số tiền thu được vào ngày tới hạn của một chứng khoán được đầu tư hết.
- Cú pháp:
=RECEIVED(settlement, maturity, investment, discount, basis)
Trong đó: discount là tỷ suất chiết khấu, các tham số khác tương tự hàm INTRATE
Ví dụ: Tính số tiền thu được vào ngày tới hạn của một tín phiếu kho bạc được đầu tư hết có ngày thanh toán là 18/05/2004, ngày tới hạn là 18/07/2006, tiền đầu tư là 20 000$, tỷ suất chiết khấu là 5.85%, cơ sở là 1.
Sử dụng hàm RECEIVED ta có:
=RECEIVED("05/18/04","07/18/06",20000,5.85%,1)
=22 900.6$
6.4 Hàm DISC (Discount)
- Tính tỷ suất chiết khấu của một chứng khoán.
- Cú pháp: =DISC(settlement, maturity, pr, redemption, basis)
Trong đó:
+ pr là giá trị mỗi 100$ mệnh giá của chứng khoán
+ redemption là giá trị phải trả cho mỗi chứng khoán 100$
+ các tham số khác tương tự như ở trên
Ví dụ: Tính tỷ suất chiết khấu cho một trái phiếu được mua lại ngày 12/05/2005 có ngày tới hạn là 19/05/2006, mua 96.18$ cho mệnh giá 100$, giá trị phải trả là 100$.
Sử dụng hàm DISC ta có:
=DISC("05/12/05","05/19/06",96.18,100,1)
=0.037



 8/17/2012
8/17/2012




 Tags:
Tags: 









4 nhận xét:
hay quá , mình đang cần
mua ban nha dat gia re quan go vap tphcm
Giới thiệu bạn dự án bất động sản vay gói 30.000 tỷ với LS 5%/năm. Bạn vào tham khảo thêm thông tin nhé. Căn hộ Tanibuilding Sơn Kỳ 1 | Can ho Tannibuilding Son Ky 1
mua ban nha dat quan go vap tphcm
Thiết thực
Đăng nhận xét